Cálculo para el desbaste de una semiesfera

Mecanizando una concavidad esférica

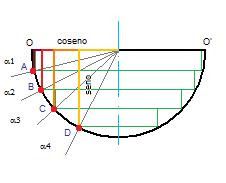
La ilustracion refleja una serie de cajeados circulares (es una vista desde el plano XZ). Sabiendo la profundidad de los cajeados y el radio de la concavidad, por trigonometría, podemos encontrar los puntos A,B,C y D. Por ejemplo si la concavidad esférica debe tener un radio de 20 mm, podemos saber la coordenada «X» del punto A (la coordenada «Z» la sabemos porque es la profundidad del cajeado). Para saber la coordenada «X» del punto A, nos bastará con usar las fórmulas del seno y del coseno.
Lo primero de todo será averiguar el ángulo alfa 1.
Sabemos que el seno de un ángulo es igual a la relación existente entre el cateto opuesto a ese ángulo y la hipotenusa. Pues según la ilustración tenemos que el seno de alfa 1= 3/20 ¿porqué 3? porque es la profundidad del cajeado circular; seno alfa 1=0.15. Para saber el ángulo que corresponde hay que hacer la inversa del seno con valor 0.15, que nos da (usando la calculadora científica) 8,626 grados.

Cálculo de la distancia

Ya tenemos el ángulo. Ahora tan solo falta averiguar la distancia existente entre el punto A y el eje de simetría. Es decir, hay que averiguar el radio que debe tener el primer cajeado circular. El coseno es la relación existente entre el cateto contiguo a ese ángulo y la hipotenusa. Por lo tanto tenemos: cos 8.626 = X/20; el coseno del ángulo 8.626 es igual a 0.988. Entonces la igualdad nos queda de la siguiente forma 0.988 = X/20. Despejando X, nos queda que X = 0.988 * 20 = 19,77. Con este ultimo paso llegamos a la conclusion de que para averiguar la cota X de los puntos A,B,C y D, podemos decir que X = cos (ángulo) * Radio.
Con estos cálculos ya tenemos el punto A. Por lo tanto ya sabemos el radio de la primera cajera. Pero…..(siempre hay un pero). Si mecanizamos la primera cajera con este radio, lo más seguro que cuando realicemos el acabado, veremos una marca, ya que en la operación de desbaste hemos llegado con el fondo de la cajera justo a un punto que también pertenece a la circunferencia. Por lo tanto, siempre es mucho mejor poner un radio con una o dos décimas de menos (en el caso de concavidades).

Bueno ahi va un ejemplo.

N020 G54
N030 T3 D3
N040 M06
N050 G0 G90 G43 X0 Y0 Z10 F200 S1000 M3
N060 G88 G99 Z2 I-3 J19.6 B3 C6 D2
N70 G88 G99 Z-2 I-6 J18.8 B3 C6 D1
N080 G88 G99 Z-5 I-9 J17.6 B3 C6 D1
N90 G88 G99 Z-8 I-12 J15.8 B3 C6 D1
N100 G88 G99 Z-11 I-15 J13 B3 C6 D1
N110 G88 G99 Z-14 I-18 J8.5 B3 C6 D1
N120 G80 G44 Z100
N130 M30