Comprobación de las soluciones para cualquier triangulo

Hola de nuevo!!!!

Cuantos meses hacía que no me dirigía a vosotr@s. Ya ha pasado demasiado tiempo sin escribir ningún artículo en programacioncnc.es y he creído conveniente que esta dinámica tenía que cambiar. Vuelvo de nuevo, y esta vez para no marchar 😉

Bueno, me dejo de tonterías y entro de lleno en este nuevo tema que os presento. El tema en cuestión está relacionado con la trigonometría, y más concretamente con la comprobación de soluciones en el cálculo de triángulos dibujados en un mismo plano (independientemente si son triángulos rectángulos o no). Es decir, cualquier tipo de triángulo, siempre y cuando esté dibujado en un mismo plano (en el XY por ejemplo).

Imaginaros que necesitáis realizar un cálculo trigonométrico en un triangulo. Lo realizáis, pero no tenéis la certeza que el resultado sea el correcto. Para colmo, no tenéis un ordenador para poder dibujar ese triángulo en AutoCAD y poder así confirmar que vuestro cálculo es correcto. Pues bien, para esos casos existe una fórmula, bueno, más que fórmula es una ecuación. Esa ecuación contiene una igualación. Si esa igualdad se cumple podemos estar seguros que nuestro resultado calculado es el correcto. Si no se cumple, algo hemos hecho mal y, por lo tanto, nuestros resultados calculados no son correctos.

La igualdad se llama ecuación de Mollweide y su representación es algo así como esto:

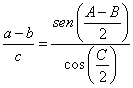
Donde las letras en minúscula representan el valor de la longitud de los catetos, mientras que las letras mayúsculas son el valor de los grados expresados en decimal. Os voy a poner un pequeño ejemplo donde podréis ver con claridad la comprobación del cálculo de un triángulo, en este caso un triángulo rectángulo. Pero podría haber sido otro tipo de triángulo.

Demostracion

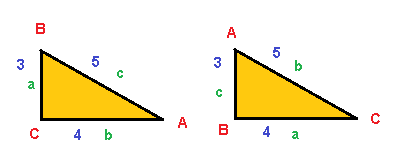
En la imagen de arriba he puesto el mismo triángulo pero «nombrando» de manera diferente a sus lados y a sus ángulos. Lo he hecho para mostrar que la igualdad en la ecuación de Mollweide siempre se va a cumplir si los cálculos son correctos.

Empiezo por el triángulo de la izquierda. Utilizando las fórmulas trigonométricas (en este enlace se refrescan algunos conceptos de trigonometría.) deduzco que el valor del ángulo B es aproximadamente igual a 53,13º decimales, mientras que el ángulo A me da un valor de aproximadamente 36,87º decimales.

Utilizando la ecuación de Mollweide en el primer triángulo tenemos:

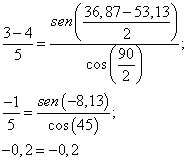
Se cumple la igualdad, por lo tanto ya tenemos la certeza que el cálculo lo hemos realizado correctamente.

Ahora realizo el mismo cálculo para el segundo triángulo manteniendo los mismos valores numéricos pero cambiando el nombre de los lados y ángulo, es decir, el lado que antes lo llamábamos a, ahora se llamará c. Lo mismo con el resto de elementos.

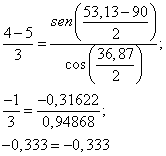
Se sigue cumpliendo la igualdad. Por lo tanto, vemos que se confirma que el cálculo está bien hecho. Si probáis cambiar un resultado de algunos de los triángulos de arriba y utilizáis la ecuación veréis que la igualdad no se cumplirá. Sois libres de probarlo si queréis ;-).

PD: Una aclaración. Cuando cambio la letra en los catetos, hay que tener en cuenta que el nombre de los ángulos debe ser el mismo que el nombre del cateto que tiene enfrente. Fijaros que el ángulo A siempre está delante del cateto a, el ángulo B siempre estará delante del cateto b…